The Impact of Quantum Computing on AI Development

Introduction

In this article I will elaborate on how quantum computing is of imminent importance for the further development of AI. The concepts of quantum computing are explained, without diving too deeply into quantum mechanics. Subsequently, unlocking of immense computational possibilities are outlined for AI and machine learning algorithms. Computer chip companies like NVIDIA are immense popular at the moment because of the AI hype. The focus is on ever faster chips to meet the growing need for AI.

However, the question arises as to how long the classic 0-1 bits in current chips will still be used. The development of quantum computing is revolutionary, because they work with a completely different concept: qubits. They can be in a superposition of states which will cause an exponential growth of parallel processing. This will be explained later on.

At the moment, there are only a few algorithms that make use of quantum computing. The most known example is Shor’s algorithm that finds the prime numbers of a large integer in polynomial time. On a classical computer, the solution time increases exponentially with the size of the integer value.

The main reason for the still limited use of quantum computers is the extreme physical operating conditions. For example, the temperature near absolute zero. They are also sensitive to errors and environmental noise. An interesting question is of course when the development is so far that the classical computer will be overtaken.

The next sections explain the qubit and its states and the difference between classical and quantum parallel computing. The architecture of hybrid systems is outlined with both classical and quantum components. Finally, future developments and their impact on the current chip market are discussed.

Difference classical Bit and Qubit

The state of a classical bit can only be binary, either 0 or 1 at a time. However, a qubit state can be in a superposition state. This means that the qubit can have non-zero probability amplitude in both its states simultaneously. This is popularly expressed as “it can be in both states simultaneously”. A qubit requires two complex numbers to describe its two probability amplitudes.

A set of N classical bits can only hold a single of its 2^N possible states at any time. Similarly, a set of N qubits is also called a qubit register. It requires 2^N complex numbers to describe its so-called superposition state vector. The next section explains the superposition principle in more detail.

Qubit States

Single Qubit

A single qubit state  |ψ⟩  can be described by a linear combination of its basis states |0⟩ and |1⟩:

where α and β are the probability amplitudes, and are both complex numbers as explained in the earlier section. Applying normalization constraint |α|2 + |β|2 = 1 and some further simplification results in the following formulas with two degrees of freedom, the two angles φ and θ:

where 

is the physically significant relative phase. When φ = π, Euler’s formula can be written as e^iπ + 1 = 0. This is known as Euler’s identity.

The possible quantum states for a single qubit is visualized using a Bloch sphere in Figure 1.

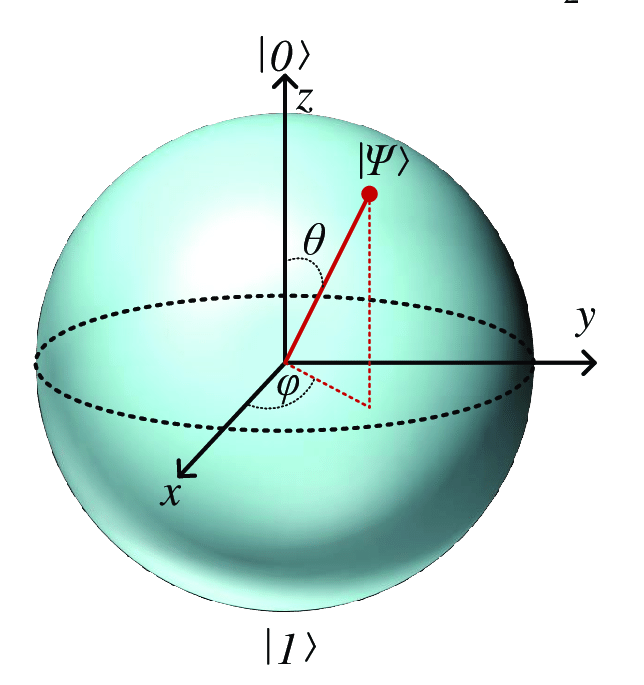
Figure 1. Bloch sphere representation of a qubit

On such a sphere, a classical bit can only be at the “North pole” or the “South pole.” These positions are at the locations |0⟩ and |1⟩ respectively. However, a pure qubit state can be represented by any point on the surface. For example, the pure qubit state

would lie on the equator of the sphere at the positive X-axis and

would lie on the equator of the sphere at the negative X-axis following Euler’s identity.

Multiple Qubit

We consider a 2-bit-wide register. A classical register can only store one of the possible values represented by  00,01,10,11(0,1,2,3).

If we consider 2 pure qubits in superpositions |a0⟩ and |a1⟩, using the quantum register definition

 

it follows that it is capable of storing all the possible values spanned by two qubits simultaneously.

Qubit Parallelism

When employing qubit systems, consider the assembly of N elementary systems. It results in a combined state with a size of 2^N. Transitions between different states are expressed by a 2^N × 2^N matrix system. This aspect of quantum parallelism is intriguing. The quantum parallelism available in a multi-qubit system scales exponentially with the number of qubits. For example, a 300-qubit system would offer parallelism greater than the number of particles in the entire universe. The next section focuses further on parallelism on classical as well as quantum systems.

Parallel Computing

Classical Computing

The previous section explained in a nutshell the superposition property of qubits. Another property is entanglement, which is the ability of linking a qubit’s state to that of another one. This property enables quantum computers to process information in a highly interconnected way. Both superposition and entanglement enable quantum computers to process multiple possibilities at once.

Refer to the previous article in which a time critical process is described using an unsupervised machine learning algorithm. All the available cores in the CPU are used to execute the process on distinct datasets in parallel. In order to achieve even better efficient use of resources, multi-threading is applied, i.e. multiple threads run simultaneously on the same core.

The code must be synchronized to handle data races and deadlocks in multi-threaded applications. Using a mutex or critical section achieves this synchronization. Below is a piece of C++ code that explains the use of a mutex.

Although it seems that the threads 1 and 2 run in parallel, it is not the case. Thread 1 is executing its code and Thread 2 must wait until the mutex is unlocked. This is because the execution of this set of code instructions should not be interrupted by the scheduler.

Quantum Computing

Quantum threads in a single QPU truly run in parallel. This stands in contrast to mimicking parallelism in a classical thread on a single core system. Quantum gates are used to generate quantum parallelism from a classical state, where no superposition exists. For instance, the Hadamard gate (H) acts on a single qubit and maps the basis states as follows:

It creates an equal superposition state if given a computational basis state. This operation corresponds to a fork operation in the classical parallelism context. In quantum computing, unitary transformations describe transitions. These transformations, along with reversibility, ensure that the total probability sums to one. They allow the reversion from a superposition of states to a classical state. This implies the transition from parallel quantum threads to a single classical thread.

Other examples of quantum gates which have the capability of creating superposition states are: Rotation-X (RX)^[1], Rotation-Y and Root-of-NOT gate. However, the H gate serves as its inverse. This characteristic grants the H gate a critical role in all quantum algorithms. The same gate can perform fork and join operations. Figure 2 illustrates a prototypical quantum application workflow^[2].

Figure 2. Quantum application workflow

Traditional quantum algorithms usually start by initializing a classical state with a WRITE operation. They then start to spawn quantum parallelism by applying H gates using N qubits (H⊗N). For example, in a 4 qubit system (N = 4), there are 4 H gates (H1–H4). We place the corresponding qubits in superposition using a fork operation. The H gates spawn the maximum available parallelism, which is 16 quantum threads. Subsequently, the input data is encoded, typically in the quantum state’s amplitude and phases. Computational processes then execute in superposition before concluding with a READ operation (measurement). The initial phase of the algorithms maximizes quantum parallelism. To extract meaningful results, it is often necessary to prune erroneous outcomes using destructive interference.

The next section describes how a quantum system can be used alongside a classical system. We will depend on such hybrid systems for now. This is due to the limited number of qubits in a quantum system.

Hybrid Systems

Due to the physical limitations, quantum systems only operate with a few number of qubits. Hybrid systems have an architecture including both a heterogeneous system and a quantum device as shown in Figure 3.

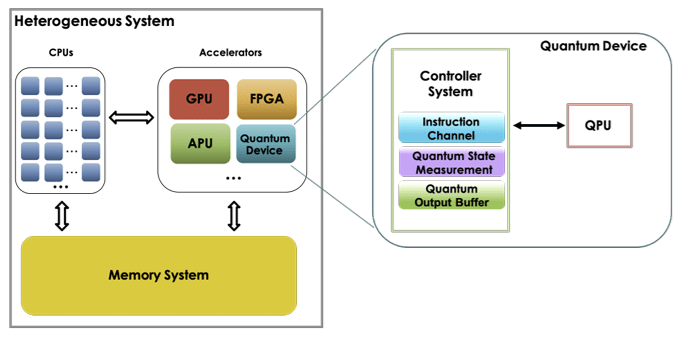
Figure 3. Hybrid classical-quantum system architecture

The left side depicts a classical computer system with multiple CPU cores, each executing multiple threads. The development environment is C++ and XASM for invoking the quantum kernel. The right side depicts a quantum device with 1 QPU. The next code shows the creation of 2 threads each invoking the quantum Bell kernel.

As discussed earlier the code needs to be made thread safe:

The above flow described in a very simplified manner how parallelism is achieved in a hybrid system. Multi-threading is applied in the heterogeneous system whereas quantum parallelism is created in the quantum device. Refer to [3] for a more in-depth description and other code examples.

Conclusion

In this article the differences between classical systems and quantum systems are discussed in detail. Parallelism in quantum computing is the key feature to tackle time consuming algorithms. The superposition and entanglement properties of qubits are the main principles for this purpose. However, the physical limitations restrict the number of qubits in a quantum system. For the time being, hybrid systems will be used which represent an architecture including classical and quantum kernels.

Future development will increase the number of qubits in quantum systems, either in single or hybrid architecture. This will allow for more algorithms to be tailored and executed in quantum mode. However, the most intriguing part is the phasing out of classical computers. The demand for ever faster chips will disappear.

AI and Machine Learning will greatly benefit from quantum computing, because there is now a pressing demand for classical hardware. The impact of quantum computing will be enormous. Algorithms will be executed exponentially faster and the demand for classic computer hardware will shrink. It will also be a leverage for cryptography, drug discovery and materials science, climate modeling and financial modeling. These topics are now left out of the scope of this article.

References

[1] Rotations on the Bloch Sphere, Ian Glendinning, 30 May 2010

[2] What is Quantum Parallelism, Anyhow?, Stefano Markidis, 12 May 2024

[3] Enabling Multi-threading in Heterogeneous Quantum-Classical Programming Models, Akihiro Hayashi, 16 March 2023

Glossary of Terms

• Quantum mechanics – The fundamental physical theory that describes the behavior of matter and of light
• Complex number – A real number x extended with an imaginary part y, in carthesian coordinates denoted by z = x + iy
• Probability amplitude – A complex number used for describing the behavior of systems
• Euler’s formula – Named after Leonhard Euler where e is the base of the natural logarithm
• CPU – Central Processing Unit in a computer system
• QPU – Quantum Processing Unit in a quantum system
• Core – Processing unit of the CPU
• Thread – Smallest sequence of programmed instructions that can be managed independently by the scheduler
• Process – Instance of a computer program running 1 or more threads
• Scheduler – Responsible for assigning resources to perform tasks in a computer program